10236. N Queens – placement
Given a chess board having n * n
cells. You need to place n queens on
the board in such a way that no queen attacks any other queen.
Input.
The size of the chess board n (1 ≤ n ≤ 10).
Output. If it is possible to place all the n
queens in such a way that no queen attacks another queen, then print n lines having n integers. The integer in i-th line and j-th column
will denote the cell (i, j)
of the board and should be 1 if a queen is placed at (i, j) and 0 otherwise. If there are
more than way of placing queens print any of them. If it is not possible to
place all n queens in the desired
way, then print “Not possible” (without quotes).
|
Sample input |
Sample output |
|
4 |
0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 0 |
SOLUTION
backtracking
Algorithm analysis
To store the information
about the arrangement of queens on the chessboard, we’ll use a
two-dimensional array mat:
·
mat[i][j]
= 1, if the queen is in position (i, j);
·
mat[i][j]
= 0, if there is no queen
is in position (i, j);
Initially there are
no queens on the board (mat[i][j]
= 0). Take the first position (1, 1) and put the queen on it (mat[1][1] = 1). Look for the next position, for example
(2, 3), that is not attacked by the first queen,
and put the second queen there. Next, we look for a position that is not attacked by two placed
queens. Such position, for
example, can be (3, 5), where we put the third queen.
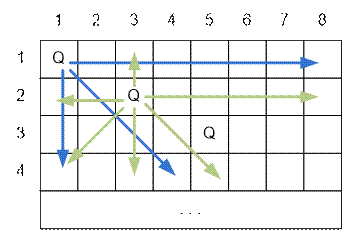
Iterate through the
positions (i, j) further and look for
one where you can put the next queen. When all the squares of the board have
been examined, and all
n queens have not been placed, start return back – backtracking. Try to
change the position of the last queen by finding another suitable place for it.
When all the positions of this queen are considered, change the position of the previous queen,
and so on, continue the search with
backtracking until all n queens
have been placed.
Algorithm realization
In the array mat, we’ll generate a
chessboard.
int mat[11][11];
Function
attacked checks
if at least one queen from position (i, j) will be attacked.
int attacked(int x, int y)
{
if (mat[x][y])return 1;
for (int i = 1; i <=
n; i++)
{
if (y - i >= 1
&& mat[x][y - i]) return 1;
if (y + i <= n
&& mat[x][y + i]) return 1;
if (x - i >= 1
&& mat[x - i][y]) return 1;
if (x + i <= n
&& mat[x + i][y]) return 1;
if (x - i >= 1
&& y - i >= 1 && mat[x - i][y - i]) return 1;
if (x + i <= n
&& y + i <= n && mat[x + i][y + i]) return 1;
if (x + i <= n
&& y - i >= 1 && mat[x + i][y - i]) return 1;
if (x - i >= 1
&& y + i <= n && mat[x - i][y + i]) return 1;
}
return 0;
}
Function print prints the chessboard.
void print(void)
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
printf("%d ", mat[i][j]);
printf("\n");
}
}
Function solve places
x more queens on the board so that
they do not attack
each other.
int solve(int x)
{
If x = 0, all n queens are placed. Print the state of the board.
if (x == 0)
{
print();
return 1;
}
Iterate
over the positions (i, j), check is it possible to
put a queen in (i, j) so that
it does not attack already
placed ones.
for (int i = 1; i <=
n; i++)
for (int j = 1; j <=
n; j++)
{
if (attacked(i, j)
== 1) continue;
Put the
queen in position (i, j).
mat[i][j] = 1;
Place x – 1 queens on the
rest of the board.
if (solve(x - 1)) return 1;
Remove the queen from position (i,
j) and make a move
backward (backtracking)
mat[i][j] = 0;
}
return 0;
}
The main part of the program. Read the board size n.
scanf("%d", &n);
Arrange n queens.
If the placement is possible, then it will be printed. Otherwise, print the message
“Not possible”.
if (!solve(n)) puts("Not possible");
Java realization
import java.util.*;
public class Main
{
static boolean mat[][];
static int n;
static boolean attacked(int x, int y)
{
if (mat[x][y]) return true;
for (int i = 1; i <= n; i++)
{
if (y - i >= 1
&& mat[x][y - i]) return true;
if (y + i <= n && mat[x][y + i]) return true;
if (x - i >= 1
&& mat[x - i][y]) return true;
if (x + i <= n && mat[x + i][y]) return true;
if (x - i >= 1
&& y - i >= 1 && mat[x - i][y - i]) return true;
if (x + i <= n && y + i <= n && mat[x + i][y + i]) return true;
if (x + i <= n && y - i >= 1
&& mat[x + i][y - i]) return true;
if (x - i >= 1
&& y + i <= n && mat[x - i][y + i]) return true;
}
return false;
}
static void print()
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
System.out.print(mat[i][j] ? 1 + " " : 0 + " ");
System.out.println();
}
}
static boolean solve(int x)
{
if (x == 0)
{
print();
return true;
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
{
if (attacked(i, j)) continue;
mat[i][j] = true;
if (solve(x - 1)) return true;
mat[i][j] = false;
}
return false;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
mat = new boolean[n+1][n+1];
if (!solve(n)) System.out.println("Not
possible");
con.close();
}
}